(Hanlon’s razor) – ”Förklara aldrig någonting med illvilja om dumhet räcker som förklaring.” – Namnet: Upphovsperson påstås vara en Robert Hanlon, men det är oklart vilken Robert Hanlon; eventuellt formulerades lagen i själva verket av författaren Robert Heinlein – mer om det i Wikipedia. – Ordet rakkniv anspelar på Ockhams rakkniv, uppkallad efter den medeltida engelska filosofen William av Ockham (se Wikipedia): krångla inte till det i onödan eller, som William uttryckte det: ”antalet storheter bör inte ökas mer än vad som är nödvändigt”.
Kategori: diverse-lagar
Bells lag
(Bell’s law eller Bell’s law of computer classes) – säger att det kommer en ny typ av datorer varje årtionde. – På 1960‑talet var det stordatorer, på 1970‑talet minidatorer, på 1980‑talet persondatorer, på 1990‑talet internetanslutna persondatorer, på 00‑talet internetanslutna mobiltelefoner och på 10‑talet surfplattor. – Lagen formulerades 1972 av Gordon Bell (länk), som då arbetade på Digital†, sedan på Microsoft Research, numera emeritus. – Gordon Bell uttryckte sig 1972 så här: ”Roughly every decade, technology advances in semiconductors, storage, networks, and interfaces enable a new, lower cost computer class also known as platform to form to serve a new need that is enabled by smaller devices e.g. less transistors per chip, less expensive storage, displays, I/O, network, and unique interface to people or some other information processing sink or source.” – Kommentatorn Ben Thompson formulerade 2014 en liknande lag – se stratechery.com/2014….
Amdahls lag
(Amdahl’s law) – ”Ett system behöver en bit in/utdata per sekund per instruktion per sekund.” – Lagen formulerades 1967 av stordator‑konstruktören Gene Amdahl (1922—2015, se Wikipedia) i föredraget ”Validity of the single processor approach to achieving large‑scale computing capabilities” (länk).
[it-system] [lagar] [ändrad 1 maj 2017]
Kryders lag
(Kryder’s law) – ”Lagringskapaciteten i magnetiska minnen fördubblas varje år.” – Uppkallad efter Mark Kryder, tidigare teknisk direktör på Seagate. Lagen beskrevs första gången 2005 i en artikel i Scientific American, klicka här (långsam länk). – Jämför med Moores lag.
[lagar] [lagringsmedier] [ändrad 29 januari 2019]
Postels lag
”Var försiktig med vad du gör, var frikostig med vad du tar emot.” – Principen handlar på hur man bör agera i ett datornätverk: man ska noggrant följa alla regler när man sänder till andra, men när man tar emot meddelanden från andra ska man vara tolerant mot eventuella fel, så länge som helheten är möjlig att tyda. – Uppkallad efter internetpionjären Jon Postel (1943—1998, se Wikipedia). Den är också känd som robusthetsprincipen (the robustness principle). (Se också robusthet.)
[internet] [lagar] [ändrad 29 oktober 2018]
Kerckhoffs princip

principen att säkerheten i ett krypteringssystem ska hänga enbart på att man hemlighåller nyckeln. Man ska däremot inte betrakta krypteringsalgoritmen som en hemlighet. – Principen formulerades 1883 av Auguste Kerckhoffs (1835—1903, namnet slutar på s, mer i Wikipedia) i boken La cryptographie militaire (länk till den franska texten). – På Kerckhoffs tid var principen främst praktiskt grundad: om säkerheten hänger på att algoritmen är hemlig, och fienden ändå får tag i algoritmen, måste man byta algoritm, vilket är svårt. Men om säkerheten hänger bara på nyckeln behöver man bara byta nyckel, vilket är enklare. Man kan också byta nyckel regelbundet, men man kan inte byta algoritm särskilt ofta. – Senare tillkom argumentet att algoritmen bör vara öppen för att den ska kunna granskas av fackfolk så att eventuella brister uppdagas. – Kerckhoffs princip är allmänt accepterad, och hemliga krypteringsalgoritmer brukar ses med misstänksamhet. Amerikanska statens officiella algoritm AES är till exempel öppen, liksom den mycket spridda RSA‑algoritmen. – En följdsats av Kerckhoffs princip är att säkerheten ökar ju färre hemligheter man har. Resonemanget kan också överföras på principen om öppen källkod. – Läs också om Schneiers lag.
[kryptering] [lagar] [ändrad 29 juni 2017]
Wirths lag
säger att ”i samma takt som hårdvaran blir snabbare så blir mjukvaran långsammare”. – Uppkallad efter Niklaus Wirth (länk), numera pensionerad forskare på tekniska högskolan i Zürich. – Jämför med Nathans fyra lagar om mjukvara.
[lagar] [niklaus wirth] [ändrad 13 januari 2020]
Brooks lag
”Nio kvinnor kan inte få ett barn på en månad.” – Även: ”Om man sätter in mer personal i ett försenat mjukvaruprojekt tar det ännu längre tid.” – På engelska: Brook’s law. – Lagen har namn efter Fred Brooks, författare till boken The Mythical Man‑Month (länk), som kom ut 1975. Han skrev där att arbetet som uträttas i ett projekt står i direkt proportion till antalet medarbetare, men projektets komplexitet ökar med kvadraten på antalet medarbetare. Alltså tar det längre tid ju fler som är med. – Fred Brooks (1931 – se länk) var anställd på IBM fram till 1965, och ledde där arbetet på operativsystemet till stordatorn System 360. 1965 blev han professor i datorvetenskap på universitetet i Chapel Hill, North Carolina (länk). – Brooks fick 1999 Turingpriset – se denna länk). – Läs också om Forresters lag.
[lagar] [projektarbete] [ändrad 13 januari 2020]
Zipfs lag
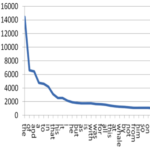
säger att frekvensen av ett värde i en stor mängd data ofta står i proportion till värdets plats i rangordningen. – Det vanligaste värdet brukar vara ungefär dubbelt så vanligt som det näst vanligaste, ungefär tre gånger så vanligt som det värde som är nummer tre på listan, och så vidare. – Lagen är uppkallad efter språkvetaren George Kingsley Zipf (1902—1950, se Wikipedia), som upptäckte att den gäller för ordfrekvenser i stora textmassor. – Exempel: i modern engelska är the det vanligaste ordet, 6,9 procent av alla ord. Näst vanligast är of med 3,6 procent och tredje vanligast är and med 2,8 procent. Som synes följer fördelningen inte Zipfs lag exakt, men det påstod Zipf inte heller att den skulle göra. Hans lag beskriver en tendens. – Lagen kallas också för Zipf‑Mandelbrots lag efter Benoit Mandelbrot†, som utvidgade principens tillämpning. Samma förhållande mellan plats i rankinglistan och frekvens av förekomster har nämligen iakttagits för andra företeelser. Man har också upptäckt att förhållandet inte alltid är rakt (alltså inte följer mönstret 1/1, 1/2, 1/3…), utan att nämnaren ofta måste multipliceras med en konstant för att lagen ska gälla. Alltså till exempel 1/4, 1/8, 1/12… – Zipfs lag är en potenslag (power law). – Lagen har också tillämpats på analys av sociala nätverk. Enkelt uttryckt: de kontakter som vi har minst kontakt med är praktiskt taget värdelösa. – Se också drakkung, långa svansen, svart svan och Paretoprincipen.
[lagar] [statistik] [ändrad 25 februari 2018]
Sturgeon’s revelation
Sturgeons insikt – ”90 procent av allting är dynga.” – Insikten drabbade science fiction-författaren Theodore Sturgeon (se Wikipedia) 1958. Han bemötte påståendet att 90 procent av all science fiction är dynga med att så är det med allting. – Kallas ibland för Sturgeons lag, men det är namnet på en annan lag, som lyder ”Nothing is always absolutely so”.
[lagar] [ändrad 13 november 2017]