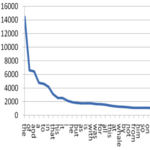
säger att frekvensen av ett värde i en stor mängd data ofta står i proportion till värdets plats i rangordningen. – Det vanligaste värdet brukar vara ungefär dubbelt så vanligt som det näst vanligaste, ungefär tre gånger så vanligt som det värde som är nummer tre på listan, och så vidare. – Lagen är uppkallad efter språkvetaren George Kingsley Zipf (1902—1950, se Wikipedia), som upptäckte att den gäller för ordfrekvenser i stora textmassor. – Exempel: i modern engelska är the det vanligaste ordet, 6,9 procent av alla ord. Näst vanligast är of med 3,6 procent och tredje vanligast är and med 2,8 procent. Som synes följer fördelningen inte Zipfs lag exakt, men det påstod Zipf inte heller att den skulle göra. Hans lag beskriver en tendens. – Lagen kallas också för Zipf‑Mandelbrots lag efter Benoit Mandelbrot†, som utvidgade principens tillämpning. Samma förhållande mellan plats i rankinglistan och frekvens av förekomster har nämligen iakttagits för andra företeelser. Man har också upptäckt att förhållandet inte alltid är rakt (alltså inte följer mönstret 1/1, 1/2, 1/3…), utan att nämnaren ofta måste multipliceras med en konstant för att lagen ska gälla. Alltså till exempel 1/4, 1/8, 1/12… – Zipfs lag är en potenslag (power law). – Lagen har också tillämpats på analys av sociala nätverk. Enkelt uttryckt: de kontakter som vi har minst kontakt med är praktiskt taget värdelösa. – Se också drakkung, långa svansen, svart svan och Paretoprincipen.
[lagar] [statistik] [ändrad 25 februari 2018]